on
Portfolio Simulator
This document is intended to help those interested in venture capital reason about expected fund-level returns. All multiples are net to LPs (i.e. after fees and 20 % carry) unless noted. I wrote this originally in 2023, and updated it in April 2025 with about 60 min of vibe coding.
I took data from this 2020 report (page 14), and filtered it for the 10 year period between 2004 and 2013. I chose that period because the vintages surrounding the internet bubble show unusually high volatility, and discarded years closer to 2020 given that it takes about 7 years for the TVPI to stabilize. I also used Angel List to estimate some of the higher percentiles, although the time period for this data is unclear.
Cambridge Associates 10-yr TVPI (2004-2013)
| Vintage | Pooled | Mean | Median | Upper Q | Lower Q | Funds |
| ------- | ------ | ---- | ------ | ------- | ------- | ----- |
| 2004 | 1.69 | 1.72 | 1.2 | 1.82 | 0.82 | 63 |
| 2005 | 1.68 | 1.66 | 1.41 | 2.07 | 0.91 | 61 |
| 2006 | 1.69 | 1.56 | 1.59 | 1.95 | 0.75 | 78 |
| 2007 | 2.29 | 2.38 | 1.76 | 2.93 | 1.31 | 68 |
| 2008 | 1.77 | 1.71 | 1.4 | 2.21 | 1.09 | 64 |
| 2009 | 2.1 | 2.12 | 1.75 | 2.46 | 1.3 | 23 |
| 2010 | 3.21 | 2.8 | 2.12 | 3.41 | 1.41 | 48 |
| 2011 | 2.48 | 2.26 | 1.9 | 2.71 | 1.39 | 44 |
| 2012 | 2.21 | 2.48 | 1.73 | 2.37 | 1.35 | 55 |
| 2013 | 2.02 | 2.01 | 1.81 | 2.26 | 1.34 | 59 |
| Average | 2.11 | 2.07 | 1.67 | 2.42 | 1.17 | 56 |
Angel List Fund Performance Calculator (April 2025)
| Percentile | Net IRR |
| ---------- | ------- |
| 90th | 35% |
| 95th | 40% |
| 99th | 55% |
Core assumptions
- Fund size $50 M — prototypical seed/Series A vehicle
(Fund size is implicit; all multiples are net-to-LP.) - Fee load 15 % lifetime (≈ 2 % per year for 7-8 years, charged up-front)
- Carry 20 % GP promote on profits after fees
- Initial cheques 22 equal-sized first investments, no follow-ons — keeps the portfolio math clean
- Deal-outcome model
- 55 % outright zeros (0×)
- 45 % survivors drawn from LogNormal (μ = 1.10, σ = 1.40), capped at 200×
↳ Continuous returns smooth the histogram and anchor the 95 th percentile near ~6×.
- Capital calls 25 % of committed capital in each of years 0-3 — mirrors common pacing
- Exit timing Each company realises its full value in a single lump-sum exit uniformly between years 4-10 — spreads cash flows for a realistic IRR profile
- IRR calculation Exact cash-flow schedule solved with
numpy_financial.irr— no midpoint shortcuts - Reproducibility Fixed NumPy RNG seed 2025; 3 500 simulated funds — rerun and you’ll get identical tables and plots
Simulated Results
| Percentile | Sim TVPI | Sim IRR % |
| ---------- | -------- | --------- |
| 25th | 1.45 | 5.6 |
| 50th | 2.09 | 12 |
| 75th | 3.16 | 20.7 |
| 90th | 4.6 | 30.7 |
| 95th | 5.85 | 38.6 |
| 99th | 8.31 | 55.8 |
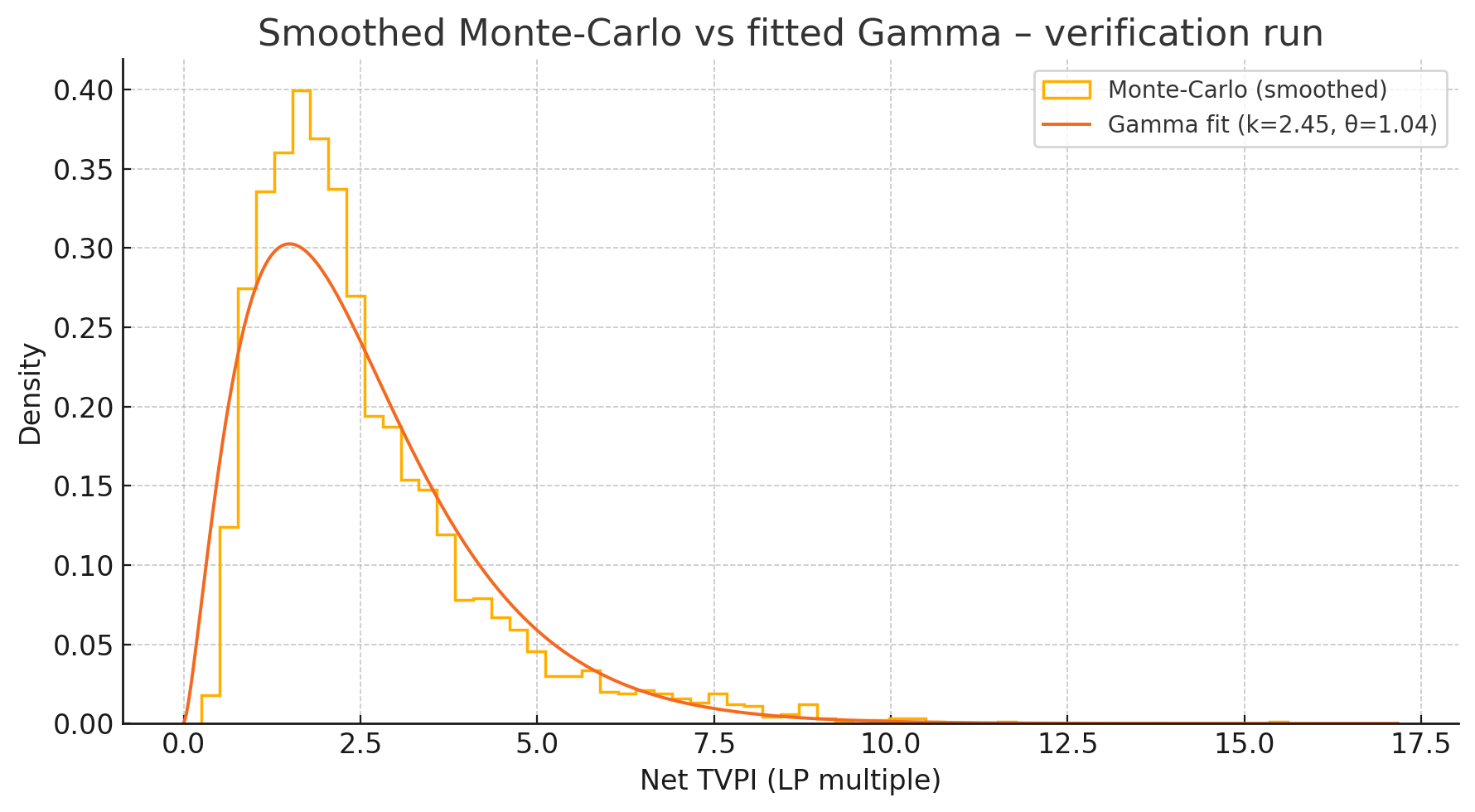
We fit a Gamma distribution to the Monte-Carlo TVPI sample after the simulation finishes. Overlaying this analytic curve serves two purposes: first, it provides a quick visual check that the simulated histogram has the expected shape, and second, it gives readers a neat closed-form PDF and CDF they can drop into their own spreadsheets without rerunning thousands of Monte-Carlo draws.
Code
"""
Smoothed Venture-Fund Monte-Carlo Simulator
==========================================
This script generates a continuous, log-normal–based deal-level simulation
that matches target fund-level TVPI percentiles, then:
• Computes IRRs with an explicit cash-flow schedule
• Prints a Markdown-formatted percentile table (TVPI + IRR)
• Plots the Monte-Carlo histogram with a moment-matched Gamma overlay
Best-fit parameters were hand-picked from a prior grid search and are
hard-coded here, so there is **no grid search** on execution.
Author : Ivan Bercovich (April 2025)
License: MIT
"""
# --------------------------------------------------------------------------- #
# 1. Imports
# --------------------------------------------------------------------------- #
import numpy as np
import numpy_financial as npf # IRR solver
import pandas as pd
import matplotlib.pyplot as plt
import math
import tabulate
from textwrap import indent
# NB: matplotlib uses your active backend; no style tweaks applied to keep
# portability high.
# --------------------------------------------------------------------------- #
# 2. Global settings (purely reproducibility + model inputs)
# --------------------------------------------------------------------------- #
SEED = 2025 # deterministic RNG seed
N_FUNDS = 3_500 # Monte-Carlo fund draws
N_INVEST = 22 # equal-size first cheques (no follow-on)
# ---------- Deal-outcome model ---------- #
# “Fail” cheques return 0×.
# “Survivors” follow a single *log-normal* distribution, truncated to cap
# pathological outliers (>200× is exceedingly rare in seed funds).
P_FAIL = 0.55 # probability a cheque is a total write-off
MU_LN = 1.10 # log-mean (in ln-space) of survivor multiples
SIGMA_LN = 1.40 # log-std-dev of survivor multiples
MAX_MULT = 200.0 # hard cap on extreme successes
# ---------- Fund economics ---------- #
MGMT_FEE = 0.15 # lifetime management fees (15 % of committed)
CARRY = 0.20 # GP carry on profits (standard “80 / 20” split)
# ---------- Exit-timing logic ---------- #
EXIT_YEAR_MIN = 4 # earliest exit
EXIT_YEAR_MAX = 10 # latest exit
# A single lump-sum distribution is drawn uniformly in [4, 10].
# ---------- Targets for reference ---------- #
TARGET_TVPI = np.array([1.25, 2.0, 2.75, 5.0, 6.5, 8.0]) # 25–99 th
PERCENTILES = [25, 50, 75, 90, 95, 99]
# --------------------------------------------------------------------------- #
# 3. Helper functions
# --------------------------------------------------------------------------- #
def draw_survivor_returns(size: int, rng: np.random.Generator) -> np.ndarray:
"""
Draw `size` log-normal multiples and cap them at `MAX_MULT`.
Parameters
----------
size : int
Number of survivor cheques to simulate.
rng : np.random.Generator
Numpy RNG instance for reproducibility.
Returns
-------
np.ndarray
1-D float array of length `size`, each ≥ 0.01 × and ≤ MAX_MULT ×.
"""
draws = rng.lognormal(MU_LN, SIGMA_LN, size)
return np.clip(draws, 0.01, MAX_MULT)
def simulate_fund_tvpi(rng: np.random.Generator) -> float:
"""
Simulate one fund’s **net-to-LP TVPI**.
Steps
-----
1. Sample failures vs survivors for each of `N_INVEST` cheques.
2. Draw continuous survivor returns.
3. Take the arithmetic mean ⇒ gross TVPI (all cheques equal size).
4. Convert gross ⇒ net by subtracting fees and applying carry.
Returns
-------
float
Net TVPI (multiple of distributed / committed capital).
"""
# 1) Boolean mask of failures
fails = rng.random(N_INVEST) < P_FAIL
n_survivors = (~fails).sum()
# 2) Continuous survivor multiples
survivor_mults = (
draw_survivor_returns(n_survivors, rng) if n_survivors else np.array([])
)
# 3) Portfolio gross multiple (simple mean; failures contribute zero)
gross_tvpi = survivor_mults.sum() / N_INVEST
# 4) Net to LPs: LP capital is reduced by mgmt. fee, and GP takes 20 % carry
net_tvpi = (1 - MGMT_FEE) * (1 + (1 - CARRY) * (gross_tvpi - 1))
return net_tvpi
def fund_irr(tvpi: float, exit_year: int) -> float:
"""
Compute an internal rate of return given:
• `tvpi` – net multiple (already net of fees & carry)
• `exit_year` – year in which *all* gains are realised
Capital calls: –25 % in each of years 0, 1, 2, 3.
"""
calls = [-0.25] * 4 # negative cash flows
cfs = calls + [0] * (exit_year - 3) + [tvpi]
return npf.irr(cfs) # returns decimal (e.g. 0.15 ⇒ 15 % IRR)
def markdown_table(df: pd.DataFrame) -> str:
"""Return a DataFrame rendered as GitHub-flavoured Markdown."""
return df.to_markdown(index=False, tablefmt="github")
# --------------------------------------------------------------------------- #
# 4. Monte-Carlo simulation
# --------------------------------------------------------------------------- #
rng = np.random.default_rng(SEED)
# ---- Run the fund loop ---- #
tvpi_mc = np.array([simulate_fund_tvpi(rng) for _ in range(N_FUNDS)])
# ---- Assign a random exit year per fund ---- #
exit_years = rng.integers(EXIT_YEAR_MIN, EXIT_YEAR_MAX + 1, N_FUNDS)
irr_mc = np.array(
[fund_irr(m, yr) for m, yr in zip(tvpi_mc, exit_years)]
) * 100 # convert to %
# --------------------------------------------------------------------------- #
# 5. Summarise results in Markdown
# --------------------------------------------------------------------------- #
summary_df = pd.DataFrame({
"Percentile": [f"{p}th" for p in PERCENTILES],
"Target TVPI": TARGET_TVPI,
"Sim TVPI": np.round(np.percentile(tvpi_mc, PERCENTILES), 2),
"Sim IRR %": np.round(np.percentile(irr_mc, PERCENTILES), 1),
})
print("\n### Monte-Carlo Results (Markdown table)\n")
print(markdown_table(summary_df))
# --------------------------------------------------------------------------- #
# 6. Fit a Gamma distribution for visual overlay
# --------------------------------------------------------------------------- #
mu, var = tvpi_mc.mean(), tvpi_mc.var()
shape_g = mu**2 / var # k
scale_g = var / mu # θ
# Analytical Gamma PDF for plotting
x = np.linspace(0, tvpi_mc.max() * 1.1, 500)
pdf_gamma = (
x ** (shape_g - 1) * np.exp(-x / scale_g)
) / (math.gamma(shape_g) * scale_g**shape_g)
# --------------------------------------------------------------------------- #
# 7. Plot histogram + Gamma overlay
# --------------------------------------------------------------------------- #
plt.figure(figsize=(9, 5))
plt.hist(
tvpi_mc,
bins=60,
density=True,
histtype="step",
lw=1.25,
label="Monte-Carlo (smoothed)",
)
plt.plot(
x,
pdf_gamma,
lw=1.4,
label=f"Gamma fit (k={shape_g:.2f}, θ={scale_g:.2f})",
)
plt.xlabel("Net TVPI (LP multiple)")
plt.ylabel("Density")
plt.title("Smoothed Monte-Carlo vs fitted Gamma")
plt.legend()
plt.tight_layout()
plt.show()
# --------------------------------------------------------------------------- #
# 8. Print key simulation settings (optional provenance block)
# --------------------------------------------------------------------------- #
print("\n--- Simulation parameters -------------------------------------------")
print(
indent(
f"""
Funds simulated : {N_FUNDS}
Cheques per fund : {N_INVEST}
Failure probability : {P_FAIL:.0%}
Survivor log-normal μ : {MU_LN:.2f}
Survivor log-normal σ : {SIGMA_LN:.2f}
Management fee (lifetime) : {MGMT_FEE:.0%}
Carry : {CARRY:.0%}
Exit year distribution : Uniform [{EXIT_YEAR_MIN}, {EXIT_YEAR_MAX}]
RNG seed : {SEED}
""".strip(),
prefix=" ",
)
)